碟形弹簧型式品种繁多，设计计算方法也有数十种之多。这里只介绍普通等截面碟形弹簧的标准GB/T1972-2005采用的设计计算方法。

一、  碟形型式

单片碟形弹簧的结构型式分两种 ：一种是无支承面碟形弹簧（图1-a）；另一种是有支承面碟形弹簧（图1-b）。

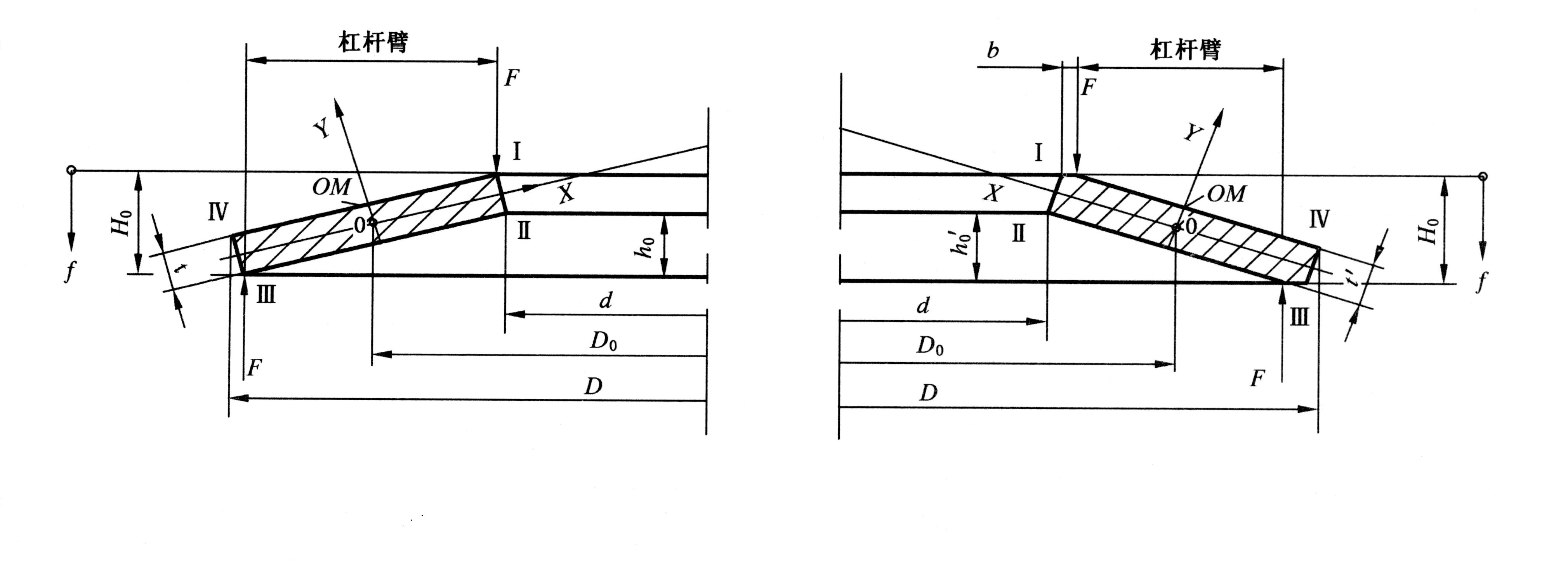
图1-a 无支承面  图1-b有支承面

二、 碟簧尺寸、参数名称及单位

碟簧尺寸、参数名称、代号及单位按表1的规定。                      

                       表   1

 三、  碟簧组合方式

    碟簧组合方式分还是为对合（图2）及叠合（图3）两种，可混合组合（图4）

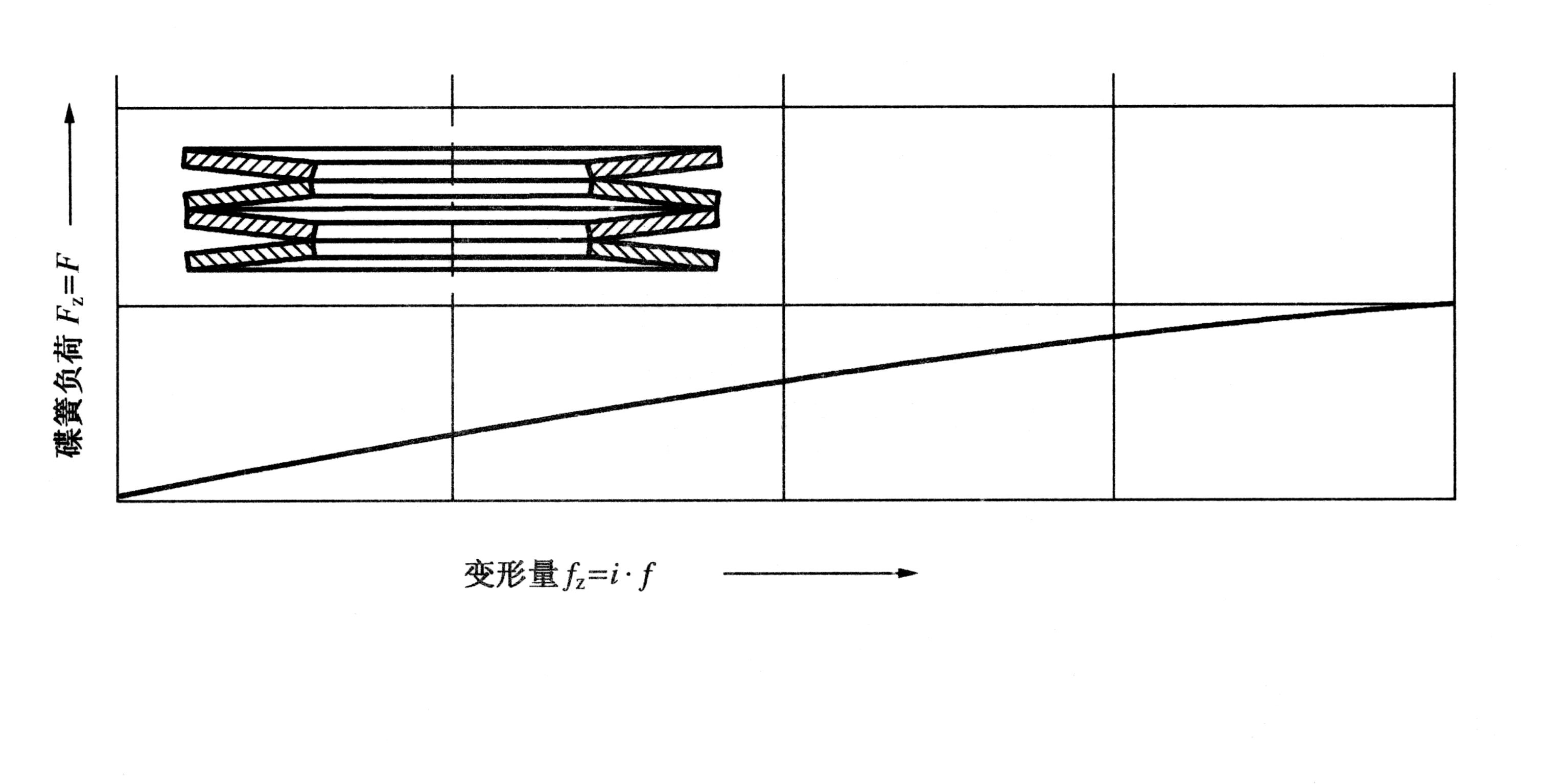
图2对合组合碟簧

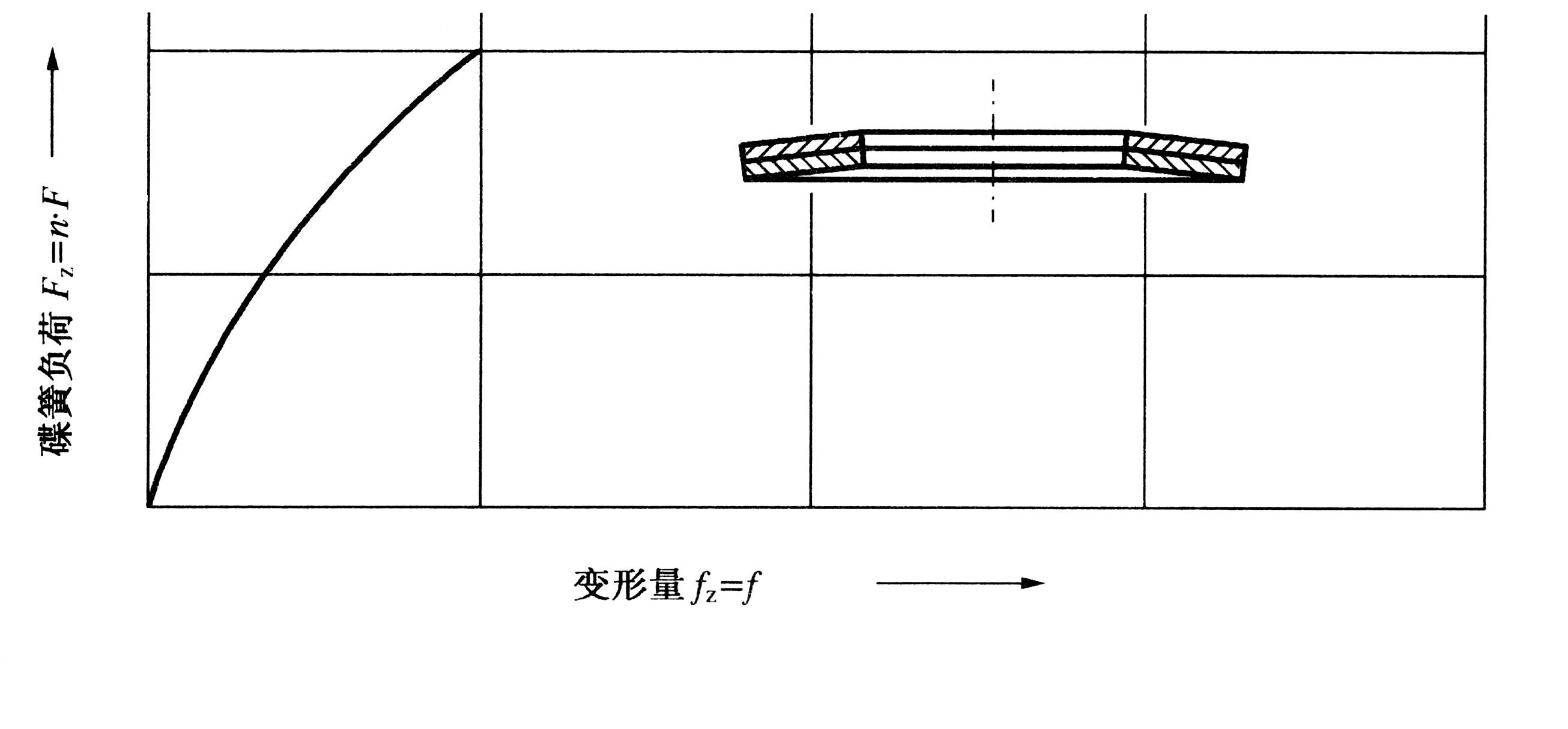
图3叠合组合碟簧

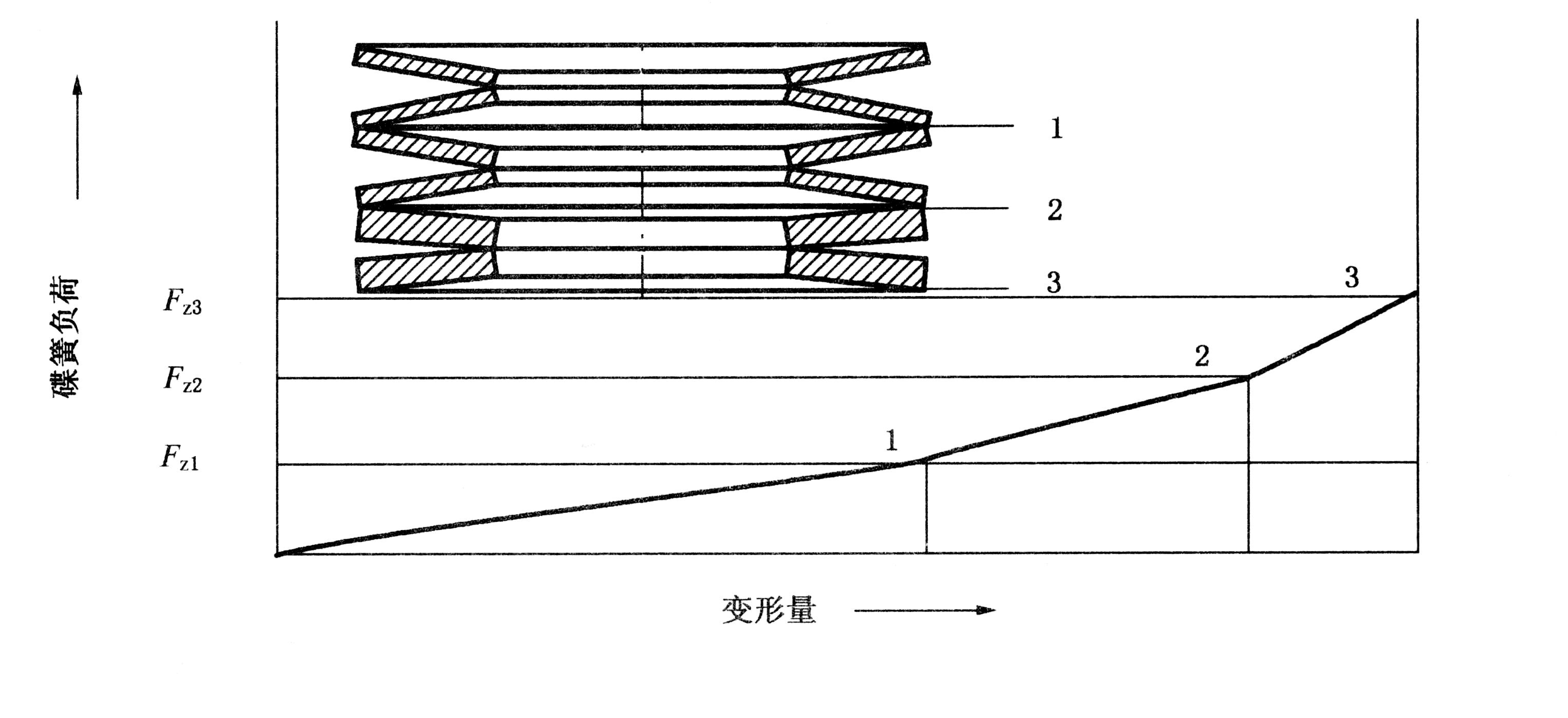
图4 可混合对合组合碟簧

四、    单片碟簧的计算公式

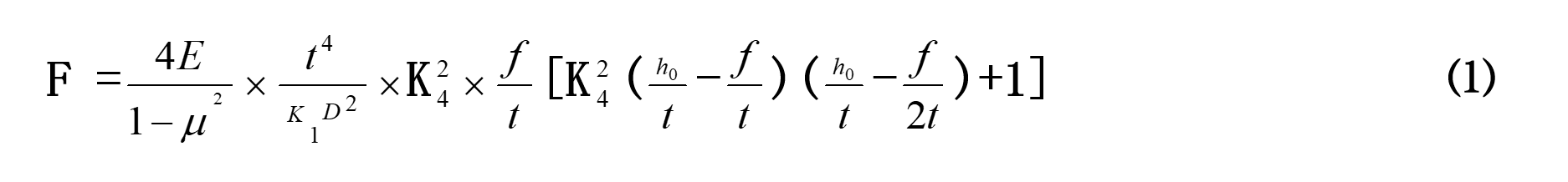
1、碟簧负荷从公式可知：

⑴、碟簧负荷与所用材料的弹性模量成正比；弹簧钢E=206×10³N/mm²；

⑵、碟簧负荷与所用材料的厚度t成三次方成正比；

⑶、碟簧负荷与碟簧外径的二次方成反比；

⑷、碟簧负荷与h₀／t、f／t有关；

⑸、碟簧负荷与µ²有关、弹簧钢的泊松比为0.3；

⑹、碟簧负荷与系数K1成反比，与系数K4的平方成正比；

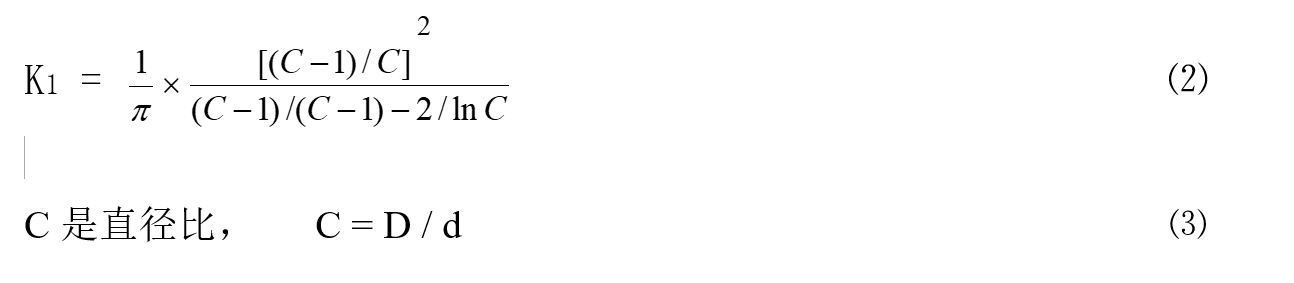
可是K1与图解、直径比有关。

碟形弹簧压平时的负荷

而C1与C2又与t´有关。

    对有支承面的碟簧，K4按（4）式计算。并在式（5）、（6）中和下文公式中以t´代替t ，以h0´= H0 - t´代替h0

2、计算应力

碟簧位置OM 处的应力

碟簧内径上表面处的应力

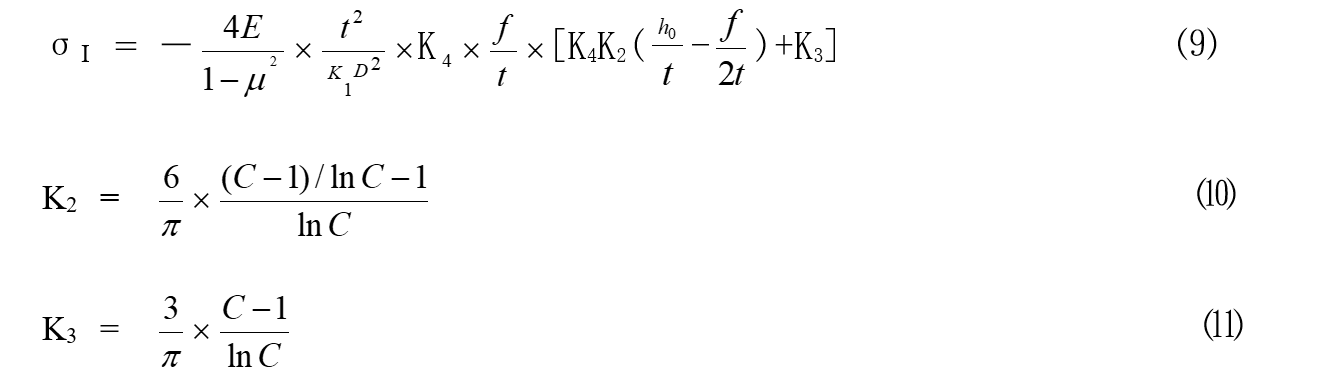
㏑是以e为底数的自然对数。

碟簧内径下表面处的应力为

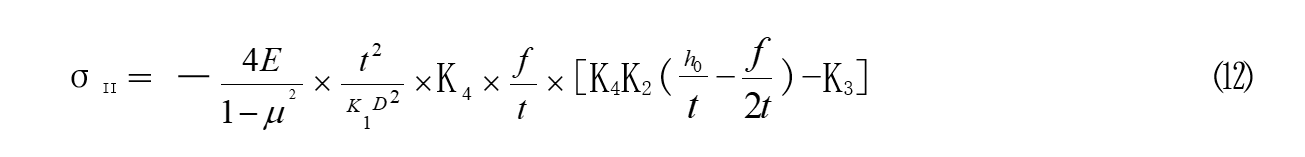
碟簧外径下表面处的应力为

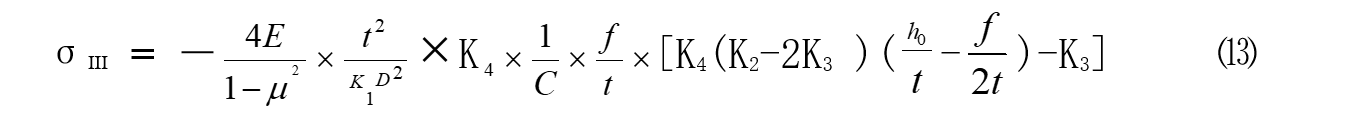
碟簧外径上表面处的应力为

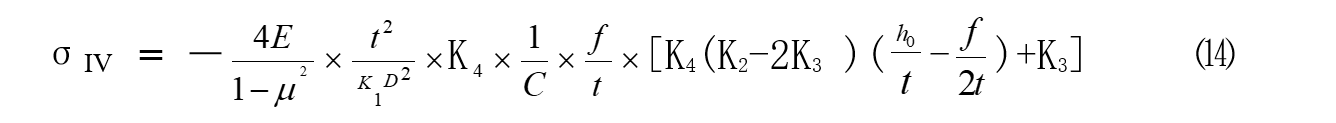
负值说明该点的压力均为压应力。

3、碟簧变形能

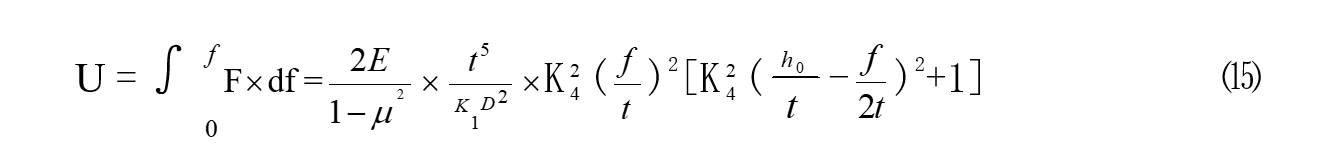
 4、碟簧刚度

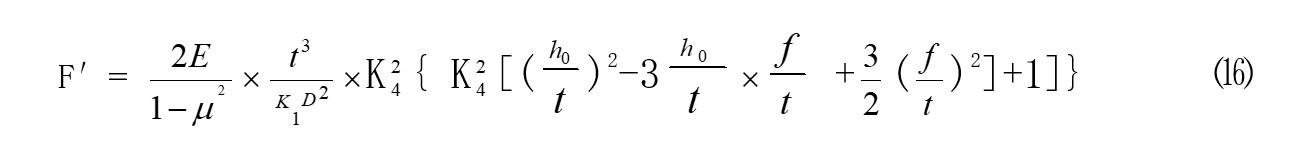
注：①、锐角矩形截面的碟簧，采用公式⑴计算碟簧负荷时，对于E=206000 N/mm²和μ=0.3的钢，其计算值与精确理论值比约高出8% - 9%,这将补偿因位置Ⅰ和Ⅲ处的杠杆臂的缩短而造成的实际碟簧负荷的增大。

    ②、D／t > 40的超薄碟簧，按⑴计算，结果数值偏大，应考虑图纸母线的弯曲。D／d < 1.8的超小直径比的碟簧，必须考虑沿半径方向杠杆臂的缩短，其计算方法应特殊考虑。

对于杠杆臂的缩短，可以影响力的大小，所以碟形弹簧就派生出有支承面的碟簧，这样无支承面碟簧在上下面的支承面的影响下，力增大了。为使标准碟簧力不变，这样就可以将原有厚度减薄，一来节约资源，二来减轻重量。所以标准碟簧的支承面宽度一般在D/150左右，其减薄比例为表2：

                      表   2

只有碟簧厚度t ≧ 6.5 mm  时才有应用，因为标准规定碟簧厚度t≧ 6.5 mm时是用锻坯加工的。

③、碟形弹簧f- F特性线不是线性的，不同的h0／t有不同的特性线。

④、碟形弹簧的理论计算公式与实际有差异。

           例如：B50碟簧计算和实测特性曲线有如图差异。

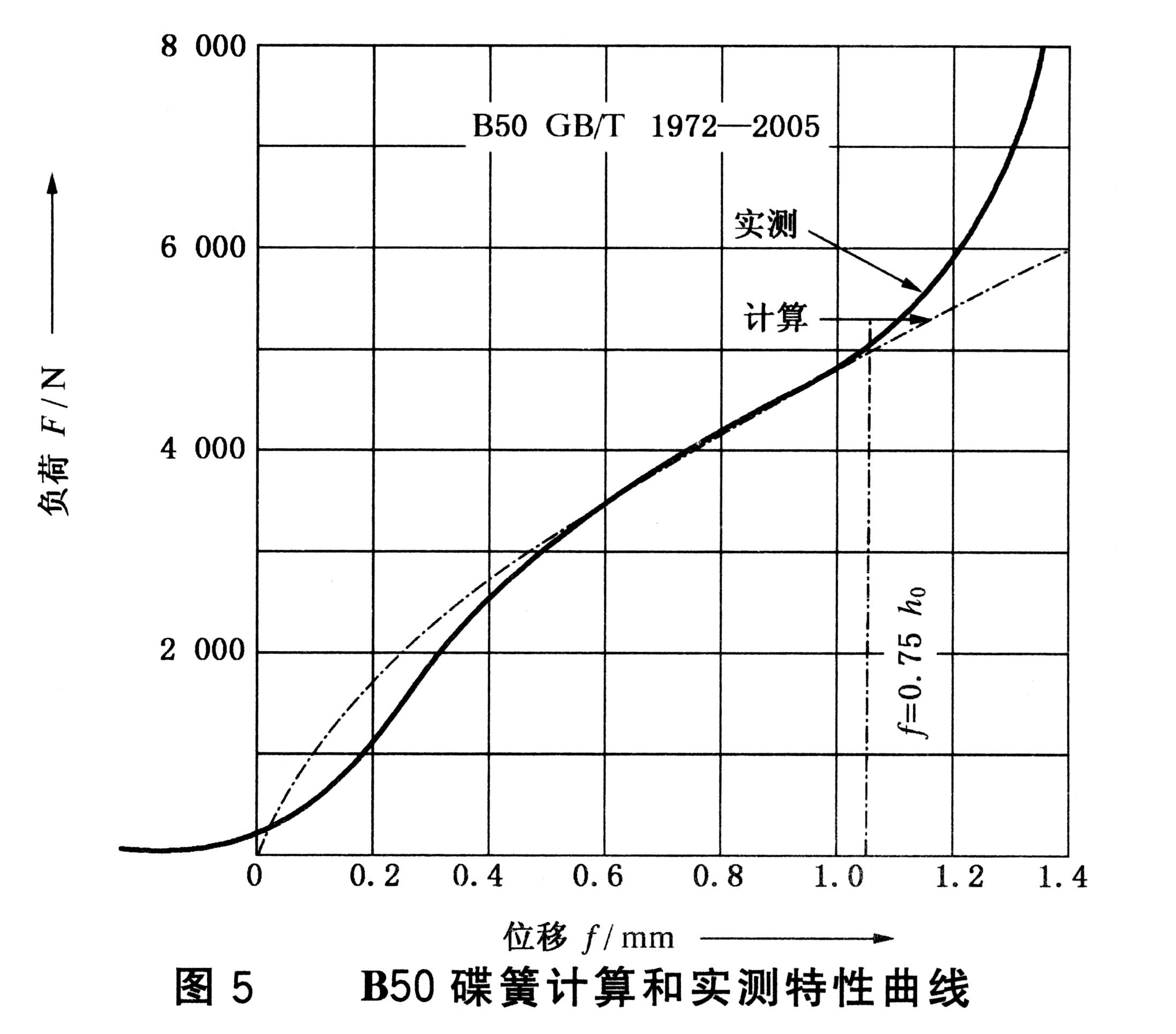
其原因有：⒈）碟簧的理论与实际有不符之处；

⒉）当f / h0 > 0.75时，由于实际杠杆臂缩短，碟簧负荷比计算值要大，这部分的计算特性曲线与实测特性曲线有较大的差别，所以标准对负荷的偏差用Ff = 0.75h0考核。

⑤、叠合组合碟簧  FZ = n · F

                 fz = f

                      Hz = H0 + (n-1) ·t

⑥、对合组合碟簧  FZ = F

                 fz = i · f

                      Hz = i · H0

⑦、复合组合碟簧  FZ = n · F

                 fz = i · f

                 Hz = i ·[ H0 + (n-1) ]·t

⑧、实际设计与使用中要考虑摩擦力，具体加减系数可参见GB / T1972-2005。

5、寿命设计

碟簧作用负荷不变或在长时间内只有偶然变化，在规定寿命内变化次数 < 1×104次，称之为静载荷。而作用在碟簧上的负荷在预加负荷F1和工作负荷F2之间循环变化，在规定寿命内变化次数 > 1×104次，称之为变负荷。

    静载荷承载前用压平负荷效验Ff = h0产生的σOM ，应接近弹簧材料的屈服极限σs ，如用标准中的弹簧钢，一般σs = 1400–1600 N/mm²。

    变载荷的寿命是由Ⅱ处或Ⅲ处的预载和终载决定的。预载产生的应力为σmin ，终载产生的应力为σmax 。

有了这两个预载，根据不同的厚度，再到GB / T1972-2005标准中三个疲劳强度曲线图中找出对应的寿命线域。如图所示。

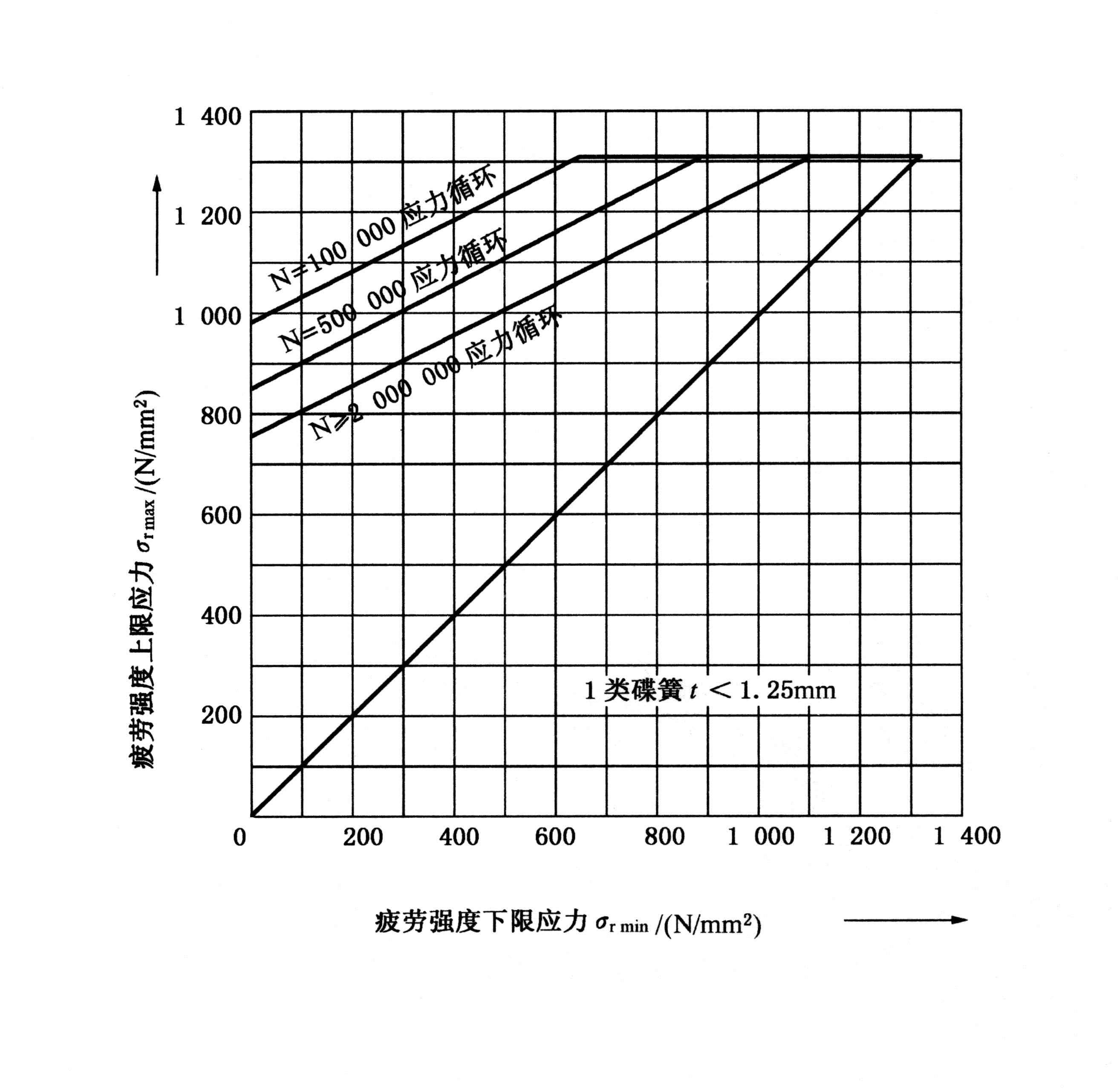
图 6     t < 1.25 mm 碟簧的疲劳强度曲线图

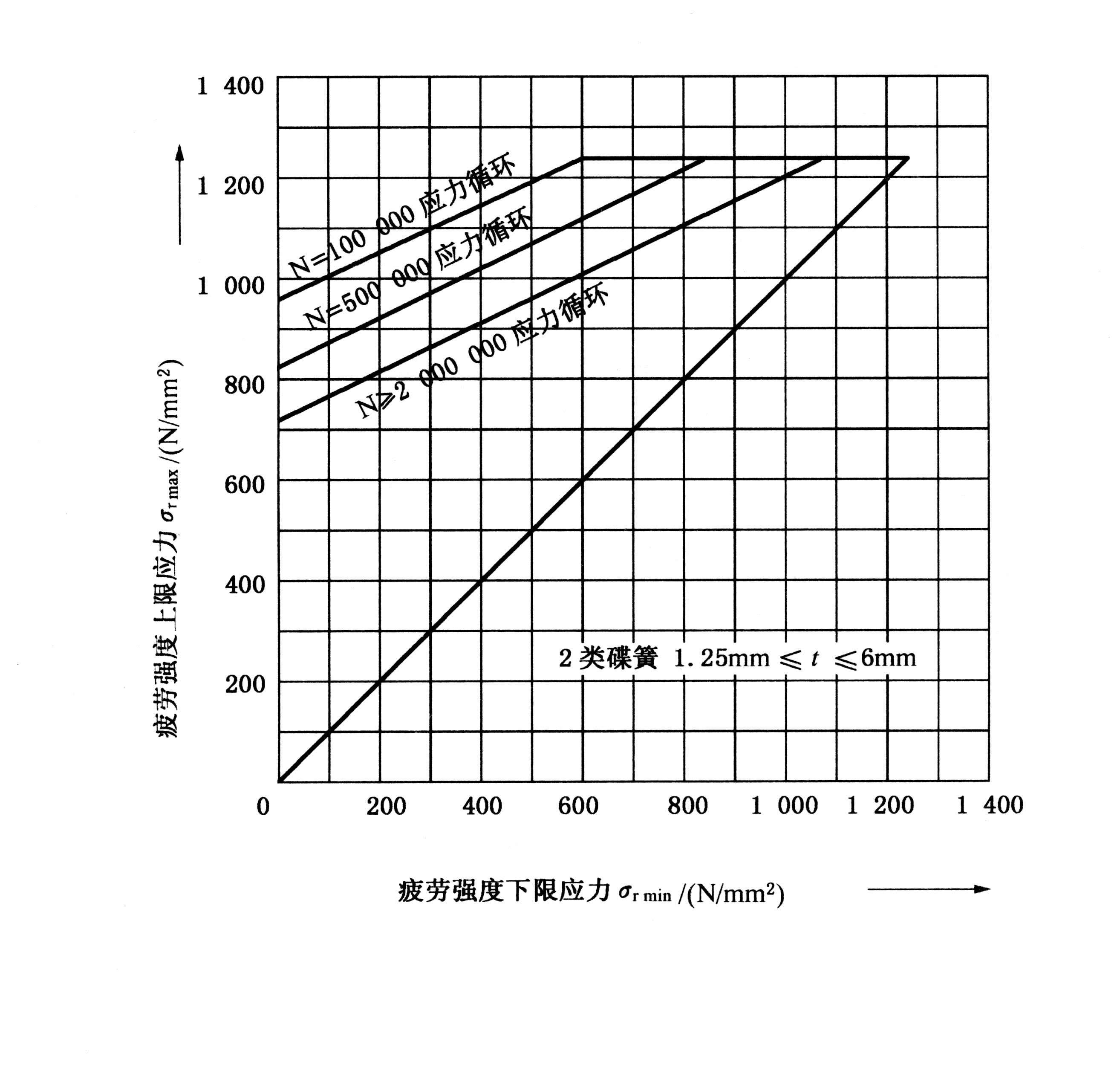
 图 7    1.25 mm ≤ t ≤ 6 mm 碟簧的疲劳强度曲线图

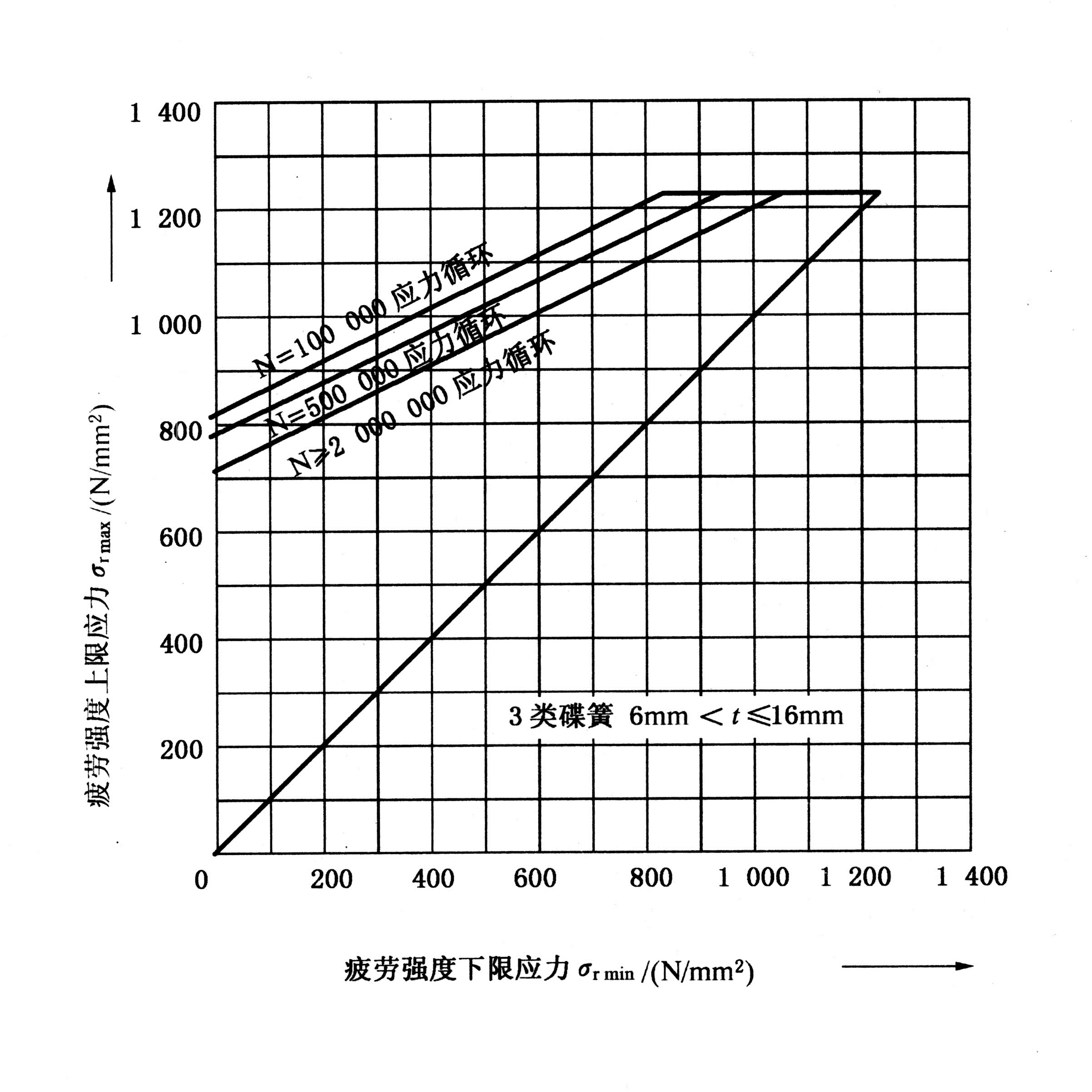
图8    6 mm < t ≤ 16 mm 碟簧的疲劳强度曲线图