环形弹簧静刚度与冲击性能分析

摘     要:  垂直减震装置是潜载导弹发射装置的重要组成部分，环形弹簧作为减震元件，是垂直减震装置的核心元件，需要满足不同工况下的减震需求。本文通过理论计算，并结合试验数据，建立环形弹簧静载和动载模型，通过分析得到静载荷作用和冲击载荷作用下环形弹簧应力应变分布情况。研究结果表明：环形弹簧有限元计算与试验结果误差不大，随着载荷的增大，应力应变也随之增大。静载工况下，外圆环最大应力出现在锥形截面上，而内圆环最大应力出现在内圆环内表面。冲击工况下，环形弹簧冲击刚度远大于静刚度值，外圆环与内圆环最大应力位置与静载状态最大应力位置相反。

关键词：环形弹簧；仿真分析；结构变形；静刚度；冲击刚度

0     引 言

环形弹簧由带有内锥面的外圆环和带有外锥面的内圆环配合而成。外圆环和内圆环沿配合圆锥面相对滑动时，接触表面具有很大的摩擦力，加载时，轴向力由表面压力和摩擦力平衡，因此，相当于减小了轴向载荷的作用，增大了弹簧刚度。卸载时，摩擦力阻滞了弹簧弹性变形的恢复，相当于减小了弹簧作用力。

环形弹簧在加载和卸载循环中，由摩擦力转化为热能所消耗的功，其大小几乎可达加载过程所做功的60%～70%，因此，环形弹簧的缓冲减震能力很高，单位体积材料的储能能力比其他类型弹簧大。环形弹簧具有变形小、压紧力大的特点,常用在空间尺寸受限制而又要求强力缓冲的场合。

针对发射装置减震大载荷工况下缓冲减震要求，选用环形弹簧既满足了大载荷冲击下缓冲减震要求，又提高了导弹发射装置纵向空间利用率，满足了垂向减震小型化需求。

本文针对环形弹簧减震特性进行静载和冲击载荷工况下有限元分析及环形弹簧静刚度特性试验分析，理论与试验相结合，进行对比分析。

1     环形弹簧静刚度及应力应变计算

1.1    环形弹簧工作原理

环形弹簧结构如图 1 所示，当轴向载荷 P 作用在圆环端面上时，在外圆环和内圆环接触的圆锥面上，作用有法向压力和摩擦力，使外圆环受拉伸而直径扩大，内圆环受压缩而直径变小，各圆环沿圆锥面相对运动而互相压入，弹簧周向尺寸缩短，即产生弹簧轴向位移 f ，而起到缓冲减震作用。

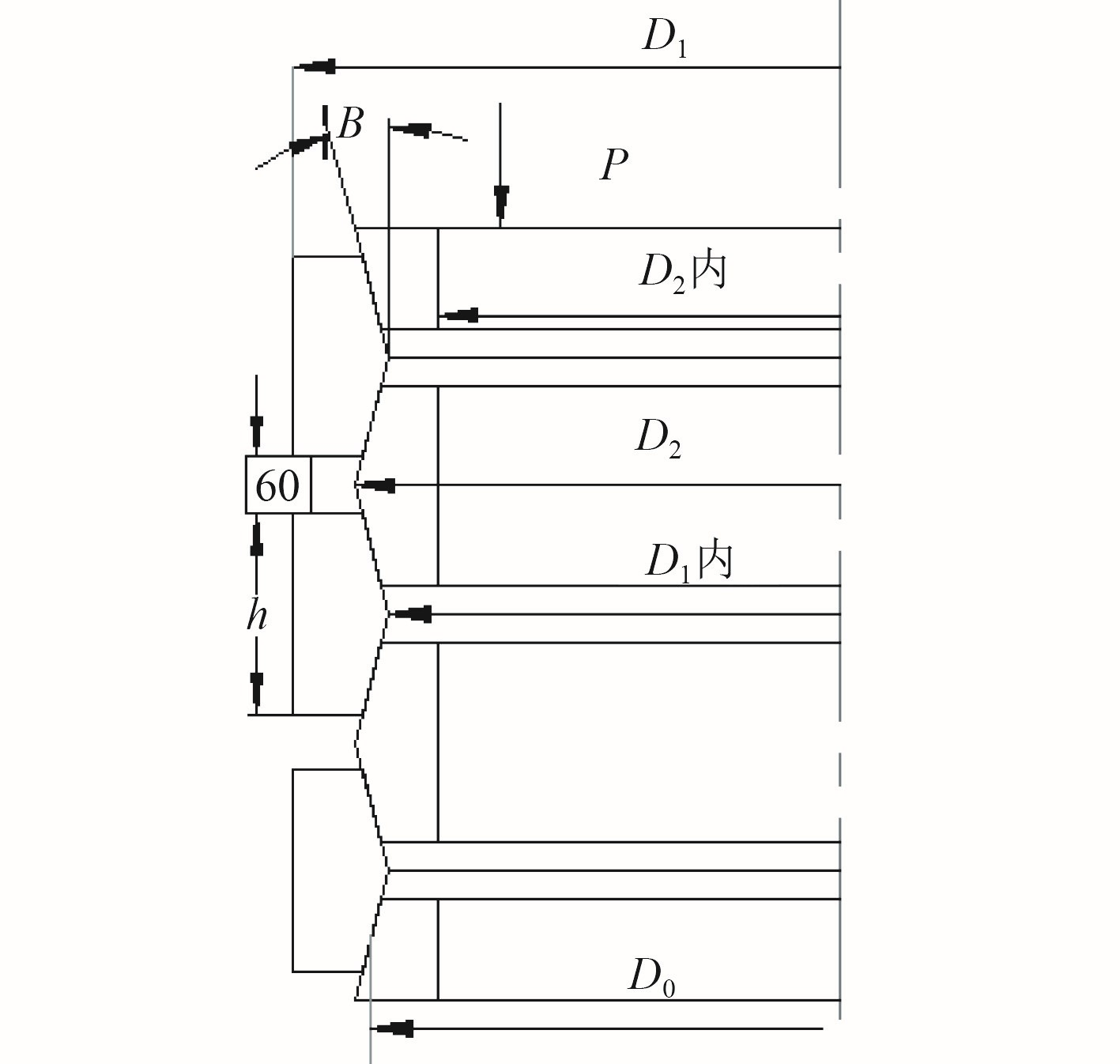
图 1   环形弹簧截面示意图

1.2    环形弹簧应力应变及静刚度计算

环形弹簧受力受很多因素的限制，包括厚度、锥面角、摩擦系数等参数，通过简化计算,得出环形弹簧最大应力、位移、静刚度值，最大应力出现在外圆环内表面。

环形弹簧在外径 φ190 mm 时，外圆环最大应力 σ1max计算公式：

其中：P 为垂向载荷；D₁ 为环形弹簧外圆环外径；D₂ 为环形弹簧内圆环外径；β为锥形角度；n 为接触面对数；δ₀为自由状态下，相邻两外圆环间间隙；ν为材料泊松比；ρ为摩擦角，取ρ=8.5^°；h 为圆环高度，取 h = 0.185D₁；D₀₁ 为环形弹簧内外圆环截面中心直径。D₀₁=D₁−b₁−0.25htan(β)，D₀₂=D₂+b₂+0.25htan(β) ， b₁ 和 b₂ 为环形弹簧内外圆环横截面厚度，b₂ = 0.25h， b₁ = 1.3b₂；A₁ 和 A₂ 分别为外圆环内圆环截面积，A₁ = hb₁+0.25h²tan(β)，A₂ = hb₂+0.25h²tan(β)；D₀ 为圆锥接触面平均直径，D₀ = 0.5(D₀₁+D₀₂)；

1.3    环形弹簧结果分析

通过计算环形弹簧在外径 φ190 mm 时，受到不同轴向力 P 情况下的环形弹簧的应力、位移及静刚度值，如表 1 所示。

表 1   环形弹簧理论计算结果

由计算结果可知，随着轴向力的增大，应力应变随之增大，静刚度值误差不大。

2     环形弹簧静刚度分析

2.1    建立环形弹簧模型

环形弹簧三维模型及边界条件如图 2 所示，环形弹簧共有 6 个接触面，由 3 个外圆环、2 个内圆环、2 个端面圆环配合组成。

图 2   环形弹簧模型及边界条件

因为环形弹簧几何形状、边界约束条件以及载荷均为轴对称结构，只建立了 1/4 结构，在保证分析精度的情况下，大大简化了模型，减小了计算量。

环形弹簧采用通用线性分析步，在各个接触面施加 surface-to-surface contact 约束，共 6 处，由于内外环的圆锥面在工作中产生相对滑动，磨擦力很大，在接触面处涂抹润滑油脂，摩擦系数设为 0.05。

在环形弹簧底部施加固定约束，侧面施加对称约束，上表面施加 Pressure 载荷。

网格划分完全使用四边形单元结构化网格，网格单元类型为 C3D8R。

图 3   网格划分类型

2.2    计算

通过计算得到环形弹簧在 10 t，20 t，30 t， 40 t 压力载荷下的变形和应力分布情况（见图 4～图 7），并计算出静刚度值和应力，如表 2 和表 3 所示。

2.3    结果分析

由应力及应变云图可知，在垂向载荷 P 作用下，外圆环受拉伸而直径扩大，内圆环受压缩而直径变小，轴向尺寸变小。

图 4   10 t 力作用下应力及位移分布图

图 5   20 t 力作用应力及位移云图

图 6   30 t 力作用下应力及位移云图

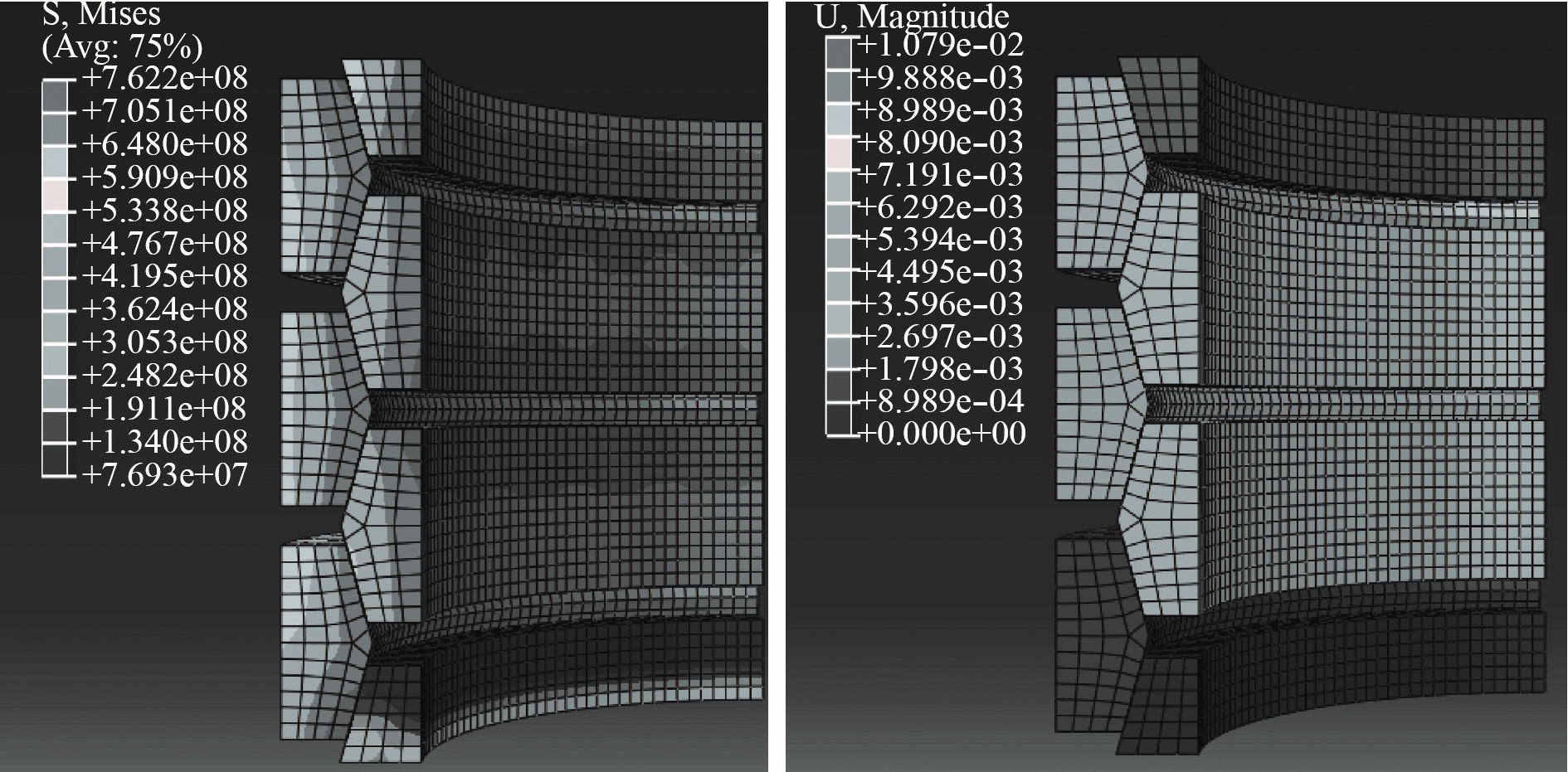
图 7   40 t 力作用下应力及位移云图

表 2   计算结果

从应力云图上可以看出，外圆环最大应力出现在锥形截面上，而内圆环最大应力不在锥形截面上，而在截面内，最大应力均小于许用应力 1 200 MPa。随着垂向力的增大，应力及位移随之增大，静刚度误差不大于 2%。

表 3   计算结果（应力）

3     环形弹簧静刚度试验

3.1    静刚度试验

为了检验环形弹簧的减震、吸收能量的能力，验证环形弹簧计算与实际刚度、理论计算刚度的差别，利用弹簧刚度试验机：WTB-4000，公称压力 4 000 kN，在工房对环形弹簧进行静刚度试验，环形弹簧材料选用不锈钢 17-4PH，环形弹簧接触面涂抹润滑油脂，减小接触面摩擦力及减小损伤。由加载卸载试验数据拟合出力-变形曲线如图 8 所示，静刚度值如表 4 所示。

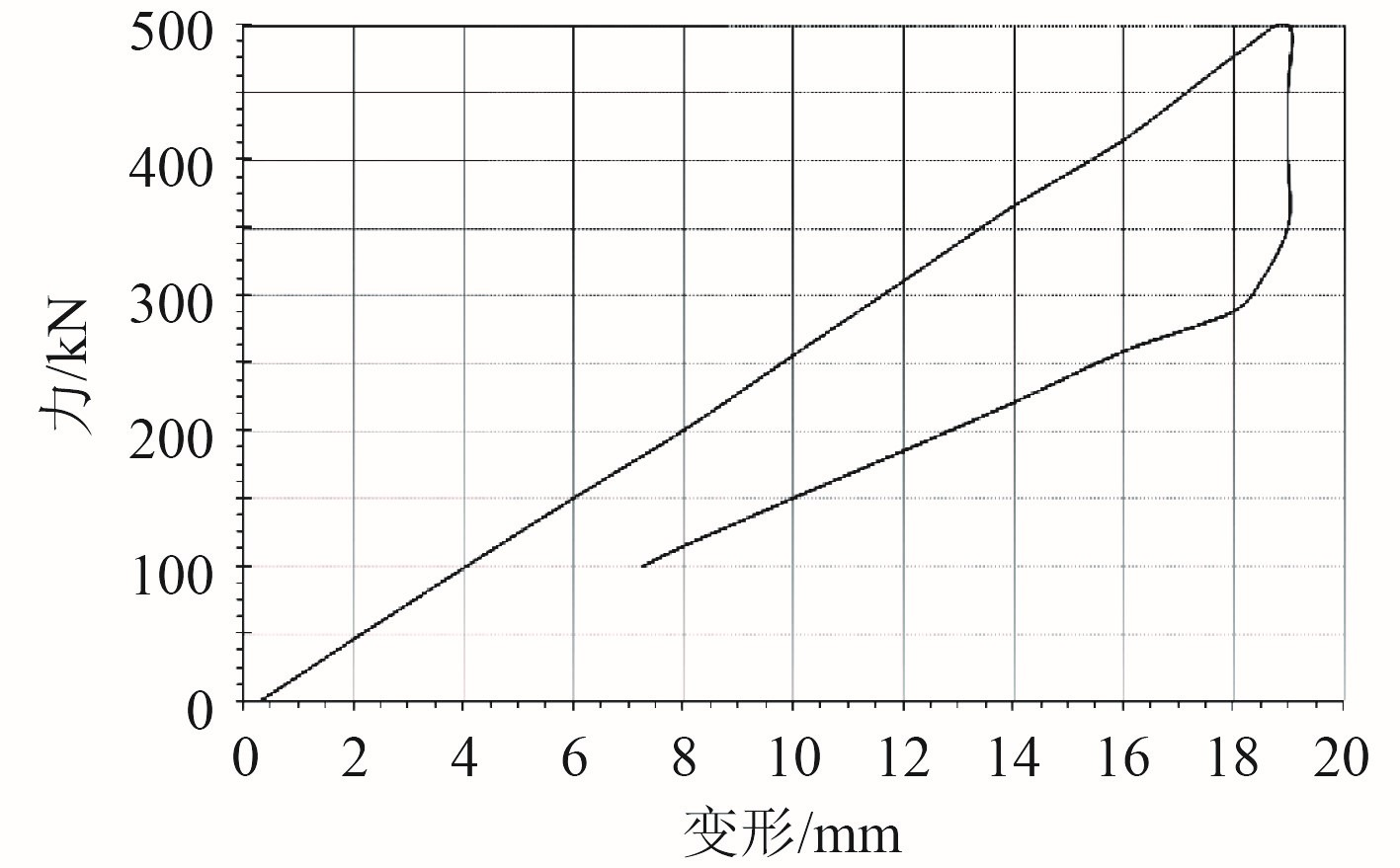
图 8   静刚度曲线图

表 4   试验静刚度结果

3.2    静刚度试验结果分析

试验结果与理论分析相一致，加载-卸载周期力-变形曲线表明，由于摩擦力转化为热能所消耗的功，阻滞了环形弹簧弹性变形的恢复，相当于减小了弹簧作用力，起到缓冲减震作用。其大小相当于加载过程所作功的 60%～70%，因此，单位体积材料的储能能力比其他类型弹簧要高，所以环形弹簧常用在空间尺寸受限制而又要求强力缓冲的场合，针对发射装置空间狭小，为了提高纵向空间利用率，选用环形弹簧作为减震元件，能够很好地满足其大载荷、小空间的减震需求，实现发射装置减震小型化改进。

4     冲击性能有限元计算

由于发射装置可能遭受敌水中兵器攻击受到冲击振动载荷作用，减震装置起缓冲作用，从而使由发射装置垂直方向传给导弹的冲击振动响应值，衰减到导弹允许的范围内，以保证导弹的安全。

当发射装置受到冲击载荷时，瞬间冲击所引起的应力和变形比静载荷时要大的多，因此需要考虑环形弹簧的冲击性能。

4.1    建模

根据落锤冲击试验模型，建立环形弹簧冲击刚度模型，由于环形弹簧为轴对称结构，简化计算模型，采用二维截面建模，落锤为解析性刚性体结构。

因为冲击响应时间很短，初步分析时，最大应力时间出现在 0.03 s 左右，为减小计算量，时间设定为 0.05 s。在锥形接触面处和落锤与环形弹簧上表面接触面添加 surface-to-surface contact（Explicit）接触。

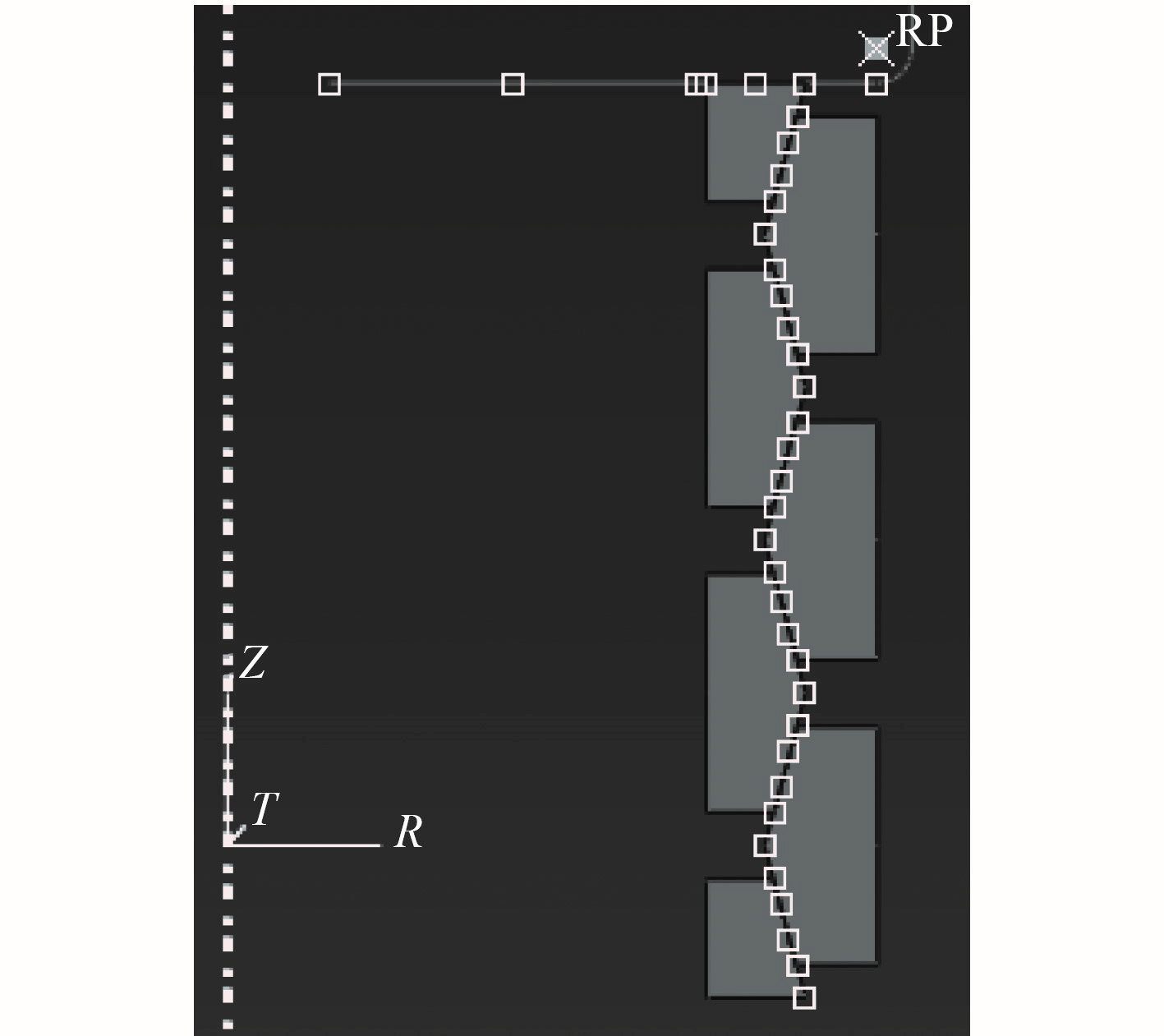
图 9   接触示意图

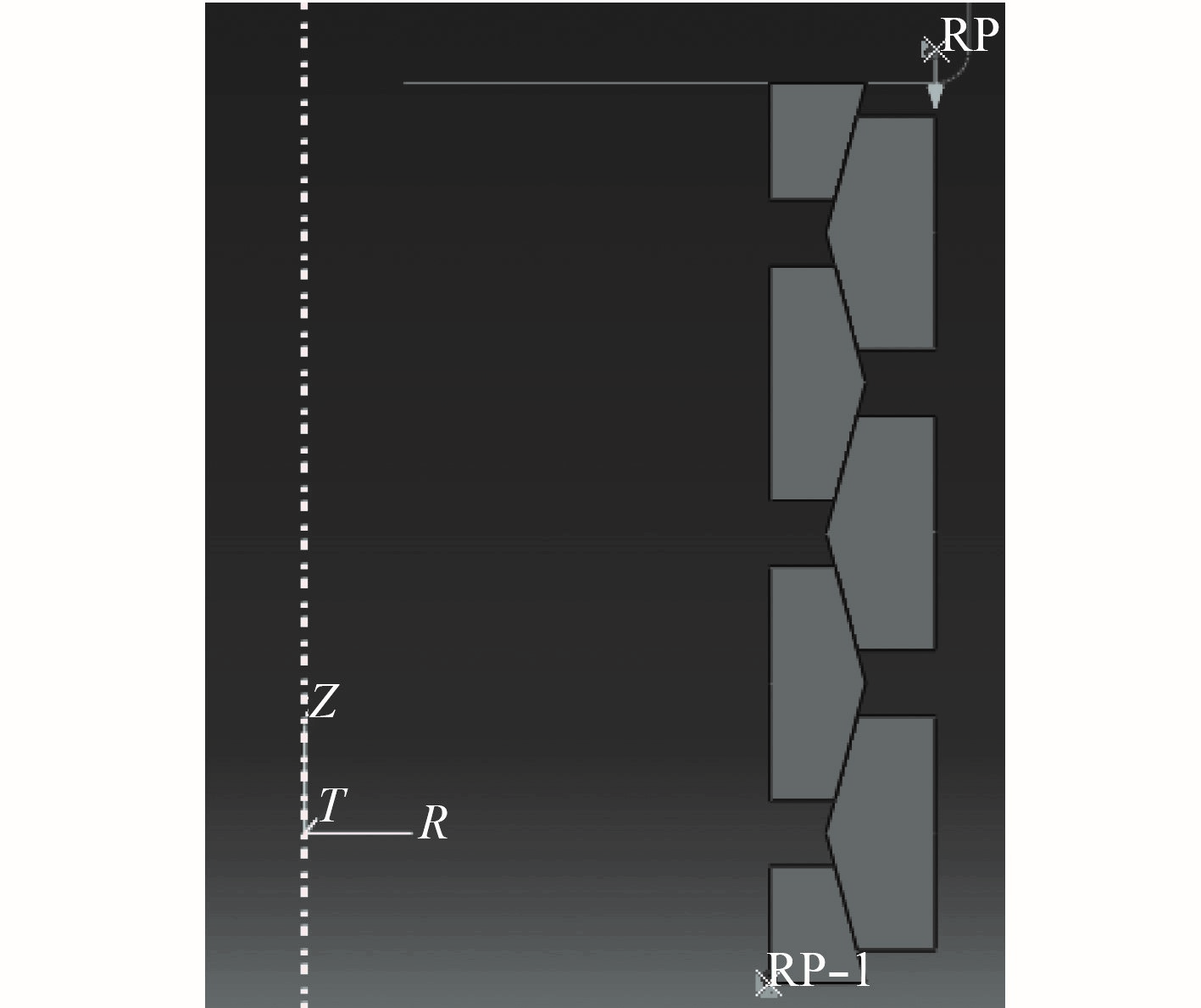
图 10   环形弹簧边界条件

     在落锤上及环形弹簧底面分别设置参考点 RP 和 RP1，并赋予 RP 垂直向下的速度，赋予 RP1 固定约束。

4.2    冲击性能结果

通过动态分析计算，得出冲击状态下环形弹簧应力应变云图如图 11 所示，冲击刚度曲线如图 12 所示。

图 11   冲击工况下应力及位移云图

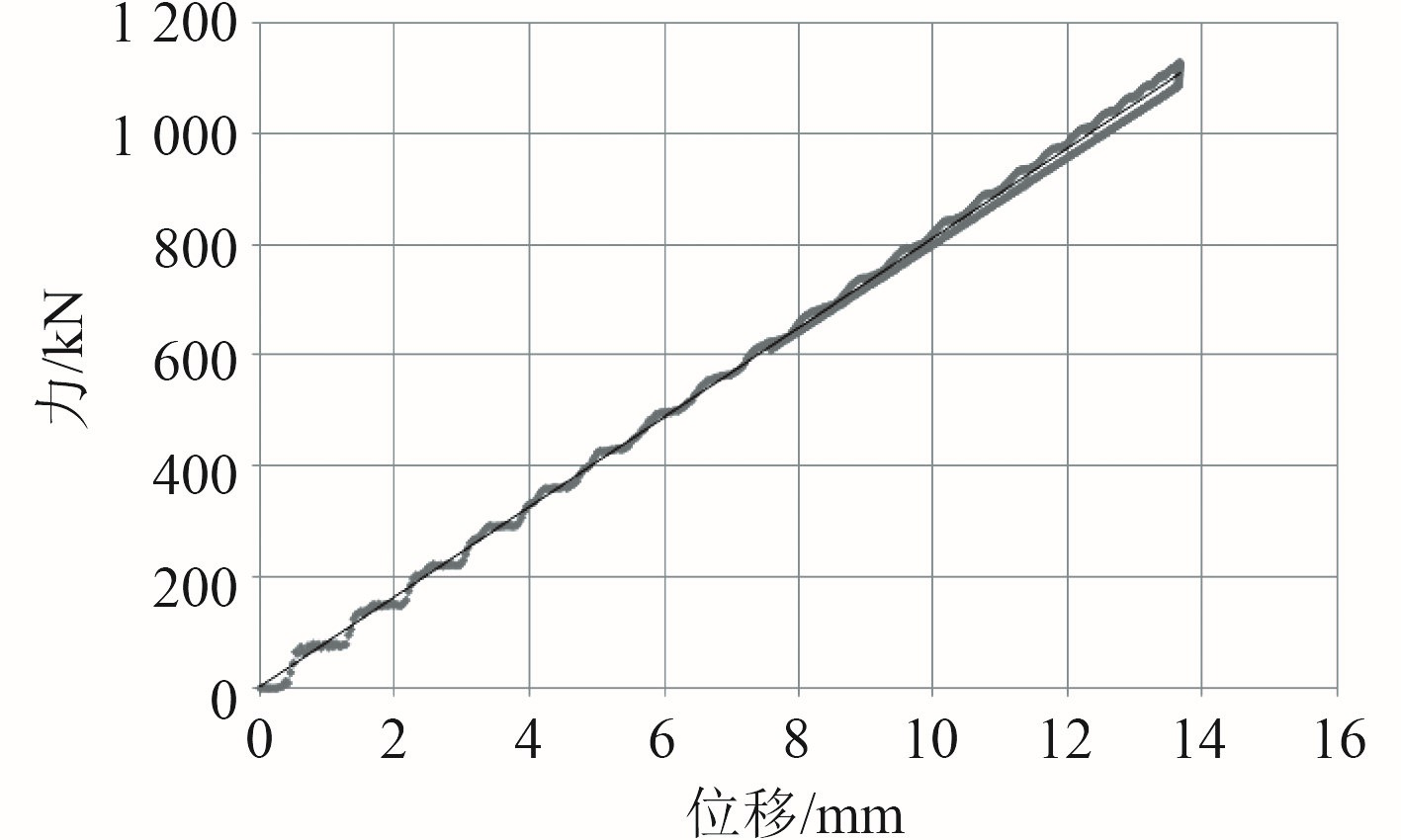
图 12   环形弹簧冲击刚度曲线

4.3    冲击性能结果分析

通过计算，得到冲击工况下应力应变云图和冲击刚度曲线。

从应力云图上可以看出，冲击状态下，内圆环最大应力出现在锥形截面上，而外圆环最大应力不在锥形截面上，而在截面内，与静载状态最大应力位置相反。

冲击刚度曲线计算得出冲击刚度约为 83 kN/mm，比静刚度要大很多。而且冲击工况下，环形弹簧会很

快的实现瞬时缓冲，起到减震作用。

5     结 语

1)本文通过理论计算，针对静载和冲击工况，与试验结果相对比，分析了环形弹簧各个工况下应力应变及刚度情况；

2)通过静载和冲击工况分析可知，冲击刚度要远大于静刚度；

3)结果与试验结果吻合度很好；

4)环形弹簧能够很好地适应瞬时缓冲。